Résumé
Ce document a pour but de montrer comment utiliser les outils de la symétrie moléculaire (ou théorie des groupes) pour résoudre l’équation de Schrödinger pour une molécule et déterminer les orbitales moléculaires. L’énergie et les coefficients des orbitales moléculaires sont obtenus par la méthode de Hückel. Le système d’étude est une molécule H3 où chaque atome d’hydrogène est au sommet d’un triangle équilatéral.
Télécharger cet article en pdf
Diagramme d’orbitales moléculaires de H3
Nous nous fixons l’objectif de résoudre l’équation de Schrödinger pour les électrons de la molécule H3 et de déterminer la fonction d’onde de l’état fondamental et son énergie. Nous utiliserons les modèles ou approximations suivantes1, 2 :
- La fonction d’onde totale est décrite comme un produit de fonctions d’onde monoélectroniques, les orbitales moléculaires, OM (modèle à particules indépendantes).
- Les OM sont décrites comme une combinaison linéaire d’orbitales atomiques, OA (méthode LCAO).
- Le modèle choisi pour l’hamiltonien du système est un hamiltonien de Hückel.
Principe
La fonction d’onde totale du système \(\Psi_F\) (configuration électronique) s’écrit :
$$ \Psi_F = \prod_{i=1}^{N_e} OM_i $$
où les OM sont les solutions de l’équation de Schrödinger pour un seul électron supposé indépendant des autres :
$$ \hat{\mathcal{H}}OM_i = \varepsilon_i OM_i $$
Dans l’approche LCAO, les OM sont exprimées dans la base des OA, l’expression générales des OM est :
$$ OM_i = \sum_{j=1}^n C_{i,j} OA_j $$
Les inconnues à déterminer sont les coefficients \(C_{i,j}\) et les énergies \(\varepsilon_i\) des OM. Les OM étant les fonctions propres de l’hamiltonien, les coefficients \(C_{i,j}\) sont en fait les coordonnées des vecteurs propres de l’hamiltonien dans la base des OA. Déterminer les OM consiste donc a diagonaliser la matrice de l’opérateur hamiltonien ce qui donnera les coefficients \(C_{i,j}\) (les vecteurs propres) et les énergies \(\varepsilon_i\) (les valeurs propres).
Lors de la résolution de l’équation de Schrödinger la diagonalisation de l’opérateur hamiltonien est un des facteurs limitant car si la matrice est de grande taille la diagonalisation sera longue. Pour faciliter la résolution nous allons utiliser les propriétés de symétrie de l’opérateur hamiltonien. En effet, l’opérateur hamiltonien commute avec toutes les opérations de symétrie de la molécule, c’est à dire que \(\hat{\mathcal{H}}\hat{\mathcal{O}}- \hat{\mathcal{O}}\hat{\mathcal{H}}=0\) souvent noté \([\hat{\mathcal{H}}, \hat{\mathcal{O}}]=0\). En effet, si la structure d’une molécule est invariante par une opération de symétrie, l’énergie totale du système et donc l’opérateur hamiltonien le sont également. Or si deux opérateurs commutent il existe un ensemble de vecteurs propres communs aux deux opérateurs. Il suffit donc de déterminer les vecteurs propres de l’un des opérateurs pour obtenir ceux de l’autre.
Les outils de la symétrie moléculaire3, 4 permettent de déterminer les vecteurs propres des opérations de symétrie. Ils donnent des combinaisons linéaires d’OA ou des ensembles de combinaisons linaires qui sont adaptées à la symétrie du problème (qui forment une base d’une représentation irréductible, RI, du groupe ponctuel). Ces combinaisons linéaires étant indépendantes les unes des autres, elles forment une nouvelle base dans laquelle la matrice de l’opérateur hamiltonien est diagonale ou bloc-diagonale. La diagonalisation de l’opérateur hamiltonien est donc réduite à la diagonalisation de blocs de tailles plus petites. Pour trouver ces combinaisons linaires nous utiliserons les équations donnée en annexes qui permettent respectivement de déterminer les symétries associées aux OA et les combinaisons linéaires d’OA adaptées à ces symétries.
Résolution dans le cas de H3
Nous allons appliquer la méthode décrite ci-dessus à la détermination des OM de la molécule H3, chaque atome d’hydrogène étant au sommet d’un triangle équilatéral. Le groupe ponctuel de symétrie est \(\mathcal{D}_{3h}\) mais pour faciliter le traitement on considérera le groupe \(\mathcal{C}_{3v}\) qui est un sous-groupe de \(\mathcal{D}_{3h}\). Un schéma de la molécule et les opérations de symétrie du groupe \(\mathcal{C}_{3v}\) sont présentés figure 1.
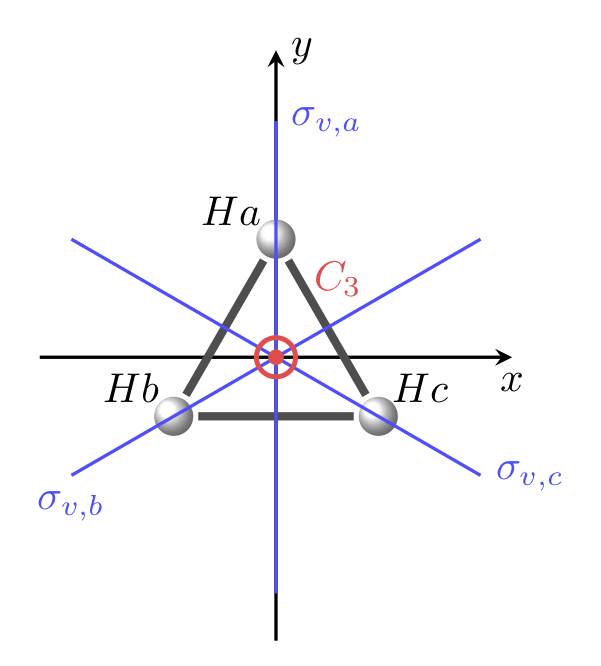 Figure 1 : Schéma de la molécule et opérations de symétrie du groupe
\(\mathcal{C}_{3v}\).
Figure 1 : Schéma de la molécule et opérations de symétrie du groupe
\(\mathcal{C}_{3v}\).
La base d’OA
Pour chaque atome d’hydrogène on considère l’OA 1s. Dans le cadre de la méthode LCAO, les OM de la molécule seront donc déterminées sous la forme :
$$ OM_i = C_{a,i} 1sH_a + C_{b,i} 1sH_b + C_{c,i} 1sH_c $$
où les indices \(a\), \(b\) et \(c\) désignent les 3 atomes d’hydrogène. Les inconnues à déterminer sont les coefficients \(C_{i,j}\) des OM.
Symétrie des OA des atomes d’hydrogène
Dans un premier temps nous devons construire la représentation \(\Gamma_H\) du groupe \(\mathcal{C}_{3v}\) dans la base des OA 1s des atomes d’hydrogène. Le plan \(\sigma_v\) qui passe par l’atome d’hydrogène X sera noté \(\sigma_v(X)\). Les résultats sont présentés dans le tableau 1. Le caractère de la représentation \(\Gamma_H\), pour une opération de symétrie, est obtenu en calculant la trace de la matrice de cette opération dans la base des trois OA 1s des atomes d’hydrogène.
Tableau 1 : Détermination de \(\Gamma_H\) et images par toutes les opérations de symétrie des OA 1s des atomes d’hydrogène
| \(\mathcal{C}_{3v}\) | E | \(\mathcal{C}^1_3\) | \(\mathcal{C}^2_3\) | \(\sigma_v(a)\) | \(\sigma_v(b)\) | \(\sigma_v(c )\) |
|---|---|---|---|---|---|---|
| \(1sH_a\) | \(1sH_a\) | \(1sH_b\) | \(1sH_c\) | \(1sH_a\) | \(1sH_c\) | \(1sH_b\) |
| \(1sH_b\) | \(1sH_b\) | \(1sH_c\) | \(1sH_a\) | \(1sH_c\) | \(1sH_b\) | \(1sH_a\) |
| \(1sH_c\) | \(1sH_c\) | \(1sH_a\) | \(1sH_b\) | \(1sH_b\) | \(1sH_a\) | \(1sH_c\) |
| \(\Gamma_H\) | 3 | 0 | 0 | 1 | 1 | 1 |
En utilisant la formule en annexes, nous obtenons la réduction de la représentation \(\Gamma_H\) en \(\Gamma_H=A_1\oplus E\). Les trois OA 1s des atomes d’hydrogène se décomposent donc en une combinaison linéaire de symétrie \(A1\) et deux autres de symétrie \(E\). Le nombre de combinaisons linéaires de chaque symétrie est lié à la dimension de la RI (1 pour \(A1\) et 2 pour \(E\), voir tableau 2 en annexes. Ces combinaisons linaires sont dites base des RI du groupe \(\mathcal{C}_{3v}\). Pour les obtenir nous appliquons un projecteur dont la formule est donnée en annexes. Les résultats obtenus sont les suivants :
$$ \begin{aligned} \hat{P}_{A1}(1sH_a) & = \frac{1}{6}\left(1sH_a + 1sH_b + 1sH_c + 1sH_a \right. \\ & \hspace*{4cm}\left. + 1sH_c + 1sH_b\right) \\ & = \frac{1}{3}\left(1sH_a + 1sH_b + 1sH_c\right) \\ \hat{P}_{E}(1sH_a) & = \frac{2}{6}\left(2\times 1sH_a - 1sH_b - 1sH_c\right) \\ \hat{P}_{E}(1sH_c) & = \frac{2}{6}\left(2\times 1sH_c - 1sH_a - 1sH_b\right) \end{aligned} $$
La fonction base de la RI \(A1\) sera noté \(1a1\) (première fonction de symétrie \(A1\)), celles qui forment une base de la RI \(E\) seront notées \((1e_1, 1e_2)\). Appliquons la condition de normalisation aux fonctions obtenues.
$$ \begin{aligned} a1 & = \mathcal{N} \left(1sH_a + 1sH_b + 1sH_c \right) \\ 1 & = \langle a1(H) \vert a1(H)\rangle \\ 1 & = N^2 \left(1sH_a + 1sH_b + 1sH_c \right)^2 \\ 1 & = N^2 \left(\frac{}{}\langle 1sH_a\vert 1sH_a\rangle + \langle 1sH_b\vert 1sH_b\rangle + \langle 1sH_c\vert 1sH_c\rangle \right.\\ & \left. + 2 \langle 1sH_a\vert 1sH_b\rangle + 2 \langle 1sH_a\vert 1sH_c\rangle + 2 \langle 1sH_b\vert 1sH_c\rangle\frac{}{}\right) \\ 1 & = N^2 \left( 3 + 6 S \right) \end{aligned} $$
Les OA étant normées \(\langle 1sH_i\vert 1sH_i\rangle = 1\). Les trois OA étant identiques et disposées sur un triangle équilatéral, notons \(S\) l’intégrale de recouvrement \(\langle 1sH_i\vert 1sH_j\rangle = S,\forall i \neq j\). Nous obtenons alors l’expression de la fonction \(1a1\) :
$$ 1a1 = \frac{1}{\sqrt{3(1 + 2S)}}\left(1sH_a + 1sH_b + 1sH_c \right) $$
Pour les fonctions bases de la représentation E, avant d’appliquer la condition de normalisation les fonctions sont orthogonalisées en faisant la somme et la différence des fonctions précédentes. Après normalisation, les fonctions obtenues sont les suivantes :
$$ \begin{cases} 1e_1 & = \displaystyle\frac{1}{\sqrt{6(1 - S)}}\left(2 \times 1sH_a - 1sH_b - 1sH_c\right) \\ 1e_2 & = \displaystyle\frac{1}{\sqrt{2(1 - S)}}\left(1sH_b - 1sH_c\right) \end{cases} $$
Le choix des combinaisons linaires bases de chaque RI n’est pas unique. Il faut choisir les plus simples ou les mieux adaptées à l’utilisation que l’on veut en faire.
Les combinaisons linaires d’orbitales atomiques ainsi obtenues sont adaptées à la symétrie du problème. Elles sont appelées orbitales de symétrie et seront notées OS par la suite.
Hamiltonien de Hückel
Écrivons la représentation matricielle de l’opérateur hamiltonien dans la base des OA 1s des trois atomes d’hydrogène. On se place dans le cadre de l’approximation de Hückel simple :
$$ \left\langle 1sH_i \vert \hat{\mathcal{H}}\vert 1sH_j \right\rangle = h_{ij} = \begin{cases} \alpha & \text{\small si i et j sont le même atome} \\ \beta & \text{\small si i et j sont adjacent} \\ 0 & \text{sinon} \\ \end{cases} $$
On obtient alors la matrice suivante :
$$ \mathbf{H} = \left(\begin{matrix} \alpha & \beta & \beta \\ \beta & \alpha & \beta \\ \beta & \beta & \alpha \\ \end{matrix}\right) $$
Exprimons maintenant cette matrice dans la base des OS (combinaisons linéaires bases des représentations irréductibles du groupe \(\mathcal{C}_{3v}\)) : \(\left\lbrace 1a1, 1e_1, 1e_2 \right\rbrace\). La matrice de passage, \(\mathbf{P}\) s’écrit :
$$ \mathbf{P} = \left(\begin{matrix} x & 2 y & 0 \\ x & -y & z \\ x & -y & -z \\ \end{matrix}\right) $$
avec \(x = 1 / \sqrt{3(1 + 2S)}\), \(y=1/\sqrt{6(1-S)}\) et \(z=1/\sqrt{2(1-S)}\). La matrice étant orthonormale, \(\mathbf{P}^{-1}=\mathbf{P}^{\intercal}\). Ainsi le changement de base s’effectue en calculant le produit \(\mathbf{P}^\intercal \mathbf{H} \mathbf{P}\) :
$$ \begin{aligned} \mathbf{P}^\intercal \mathbf{H} \mathbf{P} & = \left(\begin{matrix} 3x^2 (\alpha + 2\beta) & 0 & 0 \\ 0 & 6y^2(\alpha - \beta) & 0 \\ 0 & 0 & 2z^2(\alpha-\beta) \\ \end{matrix}\right) \\ & = \left(\begin{matrix} \displaystyle\frac{\alpha + 2\beta}{1 + 2S} & 0 & 0 \\ 0 & \displaystyle\frac{\alpha - \beta}{1 - S} & 0 \\ 0 & 0 & \displaystyle\frac{\alpha - \beta}{1 - S} \\ \end{matrix}\right) \end{aligned} $$
Solutions
Dans la base des OS, la matrice de l’opérateur hamiltonien est diagonale. Les OS et leurs valeurs propres associées représentent donc des solutions de l’équation de Schrödinger de la molécule H3.
$$ \begin{aligned} a1 & = \frac{1}{\sqrt{3(1 + 2S)}}\left(1sH_a + 1sH_b + 1sH_c \right) \\ \varepsilon_{1a1} & = \frac{\alpha + 2\beta}{1+2S} \\ \\ 1e & = \begin{cases} \displaystyle \frac{1}{\sqrt{6(1 - S)}}\left(2 \times 1sH_a - 1sH_b - 1sH_c\right) \\ \displaystyle \frac{1}{\sqrt{2(1 - S)}}\left(1sH_b - 1sH_c\right) \end{cases} \\ \varepsilon_{1e} & = \frac{\alpha-\beta}{1-S} \end{aligned} $$
Diagramme des OM de H3
À partir des résultats précédents, il est possible de tracer le diagramme d’OM de la molécule H3 qui est présenté sur la figure 2. Pour rappel, le paramètre \(\beta\) étant négatif, l’OM de plus basse énergie est l’OM \(1a1\).
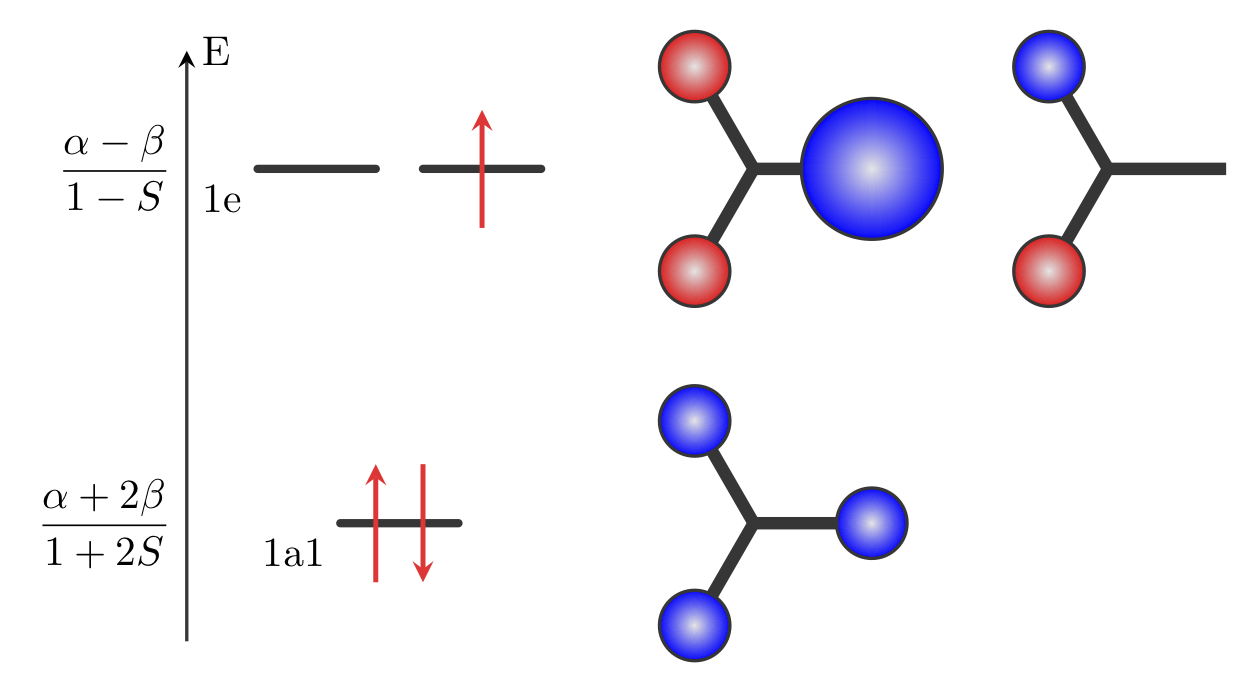 Figure 2 : Diagramme d’OM de la molécule H3
Figure 2 : Diagramme d’OM de la molécule H3
La configuration électronique de la molécule à l’état fondamental est \((1a1)^2(1e)^1\).
Annexes
Notations
- OA
-
orbitale atomique
- OS
-
orbitale de symétrie
- OM
-
orbitale moléculaire
- LCAO
-
Combinaison linéaire d’orbitales atomiques
- RR
-
Représentation réductible
- RI
-
Représentation irréductible
Outils de symétrie moléculaire
Les outils de la symétrie moléculaire pour la chimie sont basés sur les principes de la théorie des groupes. Les livres de P.H. Walton3 et F. Volatron4 sont particulièrement recommandées pour découvrir ces outils et leurs applications en chimie.
Dans ce document, nous avons utilisés deux relations issues de la théorie des groupes : la première permettant de réduire une représentation réductible en représentations irréductibles ; la seconde, un projecteur, permettant d’obtenir les fonctions bases d’une représentation irréductible.
Nombre de fois qu’intervient la représentation irréductible RI dans la décomposition de la représentation réductible RR.
$$ n_{RI} = \frac{1}{h} \sum_{operation} \chi_o(RI)\chi_o(RR) $$
où \(h\) est l’ordre du groupe et \(\chi_o(RI)\) et \(\chi_o(RR)\) sont respectivement les caractères de la RI et de la RR pour l’opération de symétrie \(o\).
Projection de la fonction \(f\) sur la représentation irréductible RI.
$$ \hat{P}_{RI}(f) = \frac{\dim_{RI}}{h}\sum_{operation} \chi_o(RI) \hat{\mathcal{O}}f $$
où \(h\) est l’ordre du groupe, \(\dim_{RI}\) la dimension de la RI et \(\hat{\mathcal{O}}f\) l’opération de symétrie appliquées à la fonction \(f\).
Table de caractère du groupe \(\mathcal{C}_{3v}\)
Tableau 2 : Table de caractères du groupe \(\mathcal{C}_{3v}\)
| \(\mathcal{C}_{3v}\) | E | 2\(\mathcal{C}_3\) | 3\(\sigma_v\) | |
|---|---|---|---|---|
| \(A_1\) | 1 | 1 | 1 | \(z\) |
| \(A_2\) | 1 | 1 | -1 | |
| \(E\) | 2 | -1 | 0 | \((x,y)\) |