Pour tracer un graphique en utilisant les coordonnées polaires le quadrillage habituel (feuille à carreaux, papier millimétré …) n’est pas adapté car il est fait pour des coordonnées cartésiennes. Les figures ci-dessous sont des guides qui facilitent le tracé de courbes en coordonnées polaires.
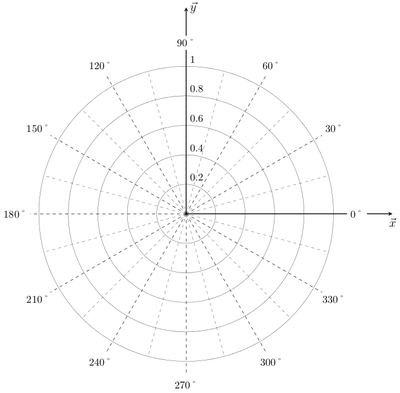Guide pour tracer des courbes en coordonnées polaires
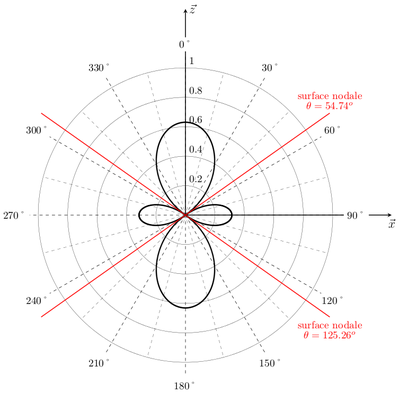
Lorsqu’on utilise les coordonnées sphériques, on peut choisir de tracer la fonction dans un plan de l’espace, par exemple le plan (xOz). En coordonnées sphériques, l’angle \(\theta\) n’est pas défini de la même manière qu’en coordonnées polaires. Il faut donc faire quelques modifications. Voici ci-dessous un exemple de tracé de la partie angulaire de l’orbitale atomique \(d_{z^2}\) dans le plan (xOz) en coordonnées sphériques.
Orbitale atomique dz2 tracée avec tikz
Le fichier polar_graph.tex ci-dessous contient :
- Le guide pour tracer des courbes en coordonnées polaires
- Le guide pour tracer des courbes en coordonnées sphériques dans le plan (xOz)
- L’exemple du dessin de la partie angulaire de l’orbitale atomique \(d_{z^2}\)
Fichier source : polar_graph.tex
Ci-dessous, un script en python qui permet de faire un graphique en coordonnées polaires en utilisant la librairies matplotlib.
#!/usr/bin/env python3
"""
plot the angular part of the dz2 AO
here theta is the polar angle, not the theta angle of spheric coordinate
"""
import numpy as np
import matplotlib.pyplot as plt
def Y20(t):
""" Compute the Y20 values """
return np.sqrt(5. / (16. * np.pi)) * (3. * (np.cos(t))**2 - 1.)
step = 1
theta = np.radians(np.arange(0, 360, step))
Y20values = np.abs(Y20(theta))
#
# Compute nodal surface angle
#
nodalAngle = np.arccos(1. / np.sqrt(3))
#
# plot the AO and nodal surfaces
#
ax = plt.subplot(111, projection="polar")
ax.plot(theta, Y20values)
ax.plot(2 * [nodalAngle], [0, 0.7], "r", 2 * [nodalAngle + np.pi], [0, 0.7], "r",
2 * [-nodalAngle], [0, 0.7], "r", 2 * [-nodalAngle + np.pi], [0, 0.7], "r")
ax.set_theta_zero_location("N")
plt.show()
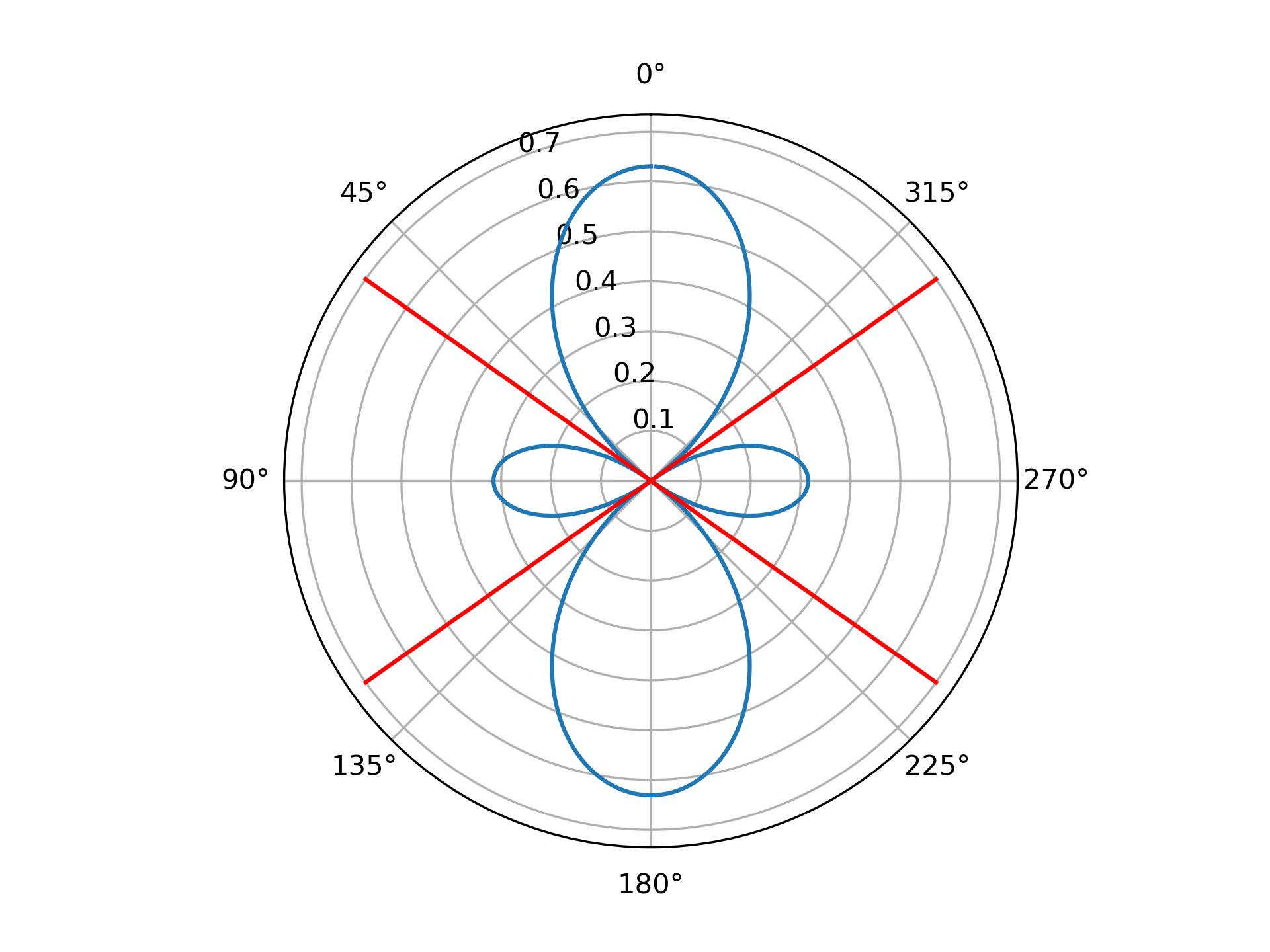Orbitale atomique dz2