Description
La méthode du bootstrap vise à évaluer l’incertitude statistique liée à l’utilisation d’un échantillon de taille limité, sans rajouter d’information supplémentaire à celles contenues dans l’échantillon dont on dispose. Cette méthode permet donc de calculer les incertitudes statistiques sur la valeur moyenne, la valeur médiane ou encore les intervalles de confiances d’une grandeur (c’est à dire l’un des estimateurs statistiques de la densité de probabilité). Dans les études réalisées par simulation moléculaire ou par chimie quantique, la taille des échantillons est limitée, notamment par le temps de calcul. La densité de probabilité est donc obtenue de manière approchée. Le bootstrap est alors bien adapté à l’évaluation des incertitudes statistiques sur les estimateurs statistiques.
La méthode
Le bootstrap est synonyme de ré-échantillonnage. On note \(x\) la variable échantillonnée. Soit \(\theta\) la vraie valeur, en général inconnue, de l’estimateur statistique (par exemple la valeur moyenne) que l’on cherche à déterminer. On note \(E_i\) un échantillon initial contenant N éléments, de valeur \(x^i_k\), obtenu par une technique d’échantillonnage quelconque à partir de l’espace complet des éléments. On note \(\theta_i\) la valeur de l’estimateur statistique \(\theta\), obtenue à partir de l’échantillon initial. La méthode du bootstrap consiste à construire \(N_b\) échantillons de bootstrap, notés \(E_b\), de la même taille que l’échantillon initial, en utilisant les éléments de l’échantillon initial. Les \(N\) éléments de l’échantillon \(E_b\), de valeur \(x^b_k\), sont choisis aléatoirement parmi les \(N\) éléments de l’échantillon \(E_i\) avec remise, c’est à dire qu’un même élément peut être choisi plusieurs fois. A chaque tirage, chaque élément de l’échantillon initial a la même probabilité \(1/N\) d’être choisi. De cette manière la densité de probabilité construite à partir des valeurs \(x^b_k\) des éléments de \(E_b\) conserve approximativement la même forme que celle construite à partir des valeurs \(x^i_k\) des éléments de \(E_i\). En effet, plus la probabilité d’obtenir une valeur donnée \(x_0\) est grande, plus le nombre d’éléments de l’échantillon \(E_i\) qui ont une valeur \(x^i_k\) proche de \(x_0\) sera grand et donc, lors de la construction des échantillons \(E_b\), la probabilité de choisir un élément de \(E_i\) dont la valeur \(x^i_k\) est proche de \(x_0\) sera grande. La figure ci-dessous résume le fonctionnement de la méthode du bootstrap.
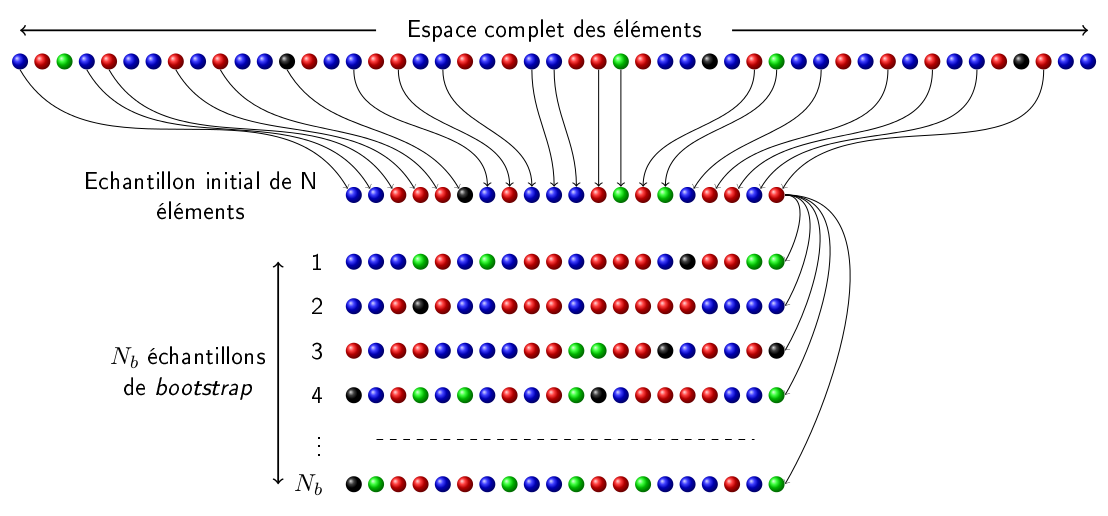
Pour chacun des \(N_b\) échantillons \(E_b\), la valeur \(\theta_b\) de l’estimateur \(\theta\) peut être calculée. On obtient ainsi la distribution \(\mathcal{D}^b(\theta)\) des valeurs de l’estimateur \(\theta\) extraites des \(N_b\) échantillons \(E_b\). D’autre part, notons \(\mathcal{D}^{all}(\theta)\) la distribution des valeurs de l’estimateur \(\theta\) extraites de tous les échantillons contenant \(N\) éléments qui peuvent être construit à partir de l’espace complet des éléments. Il a été démontré par B. Efron qu’à la limite où le nombre \(N\) d’éléments de l’échantillon initial tend vers l’infini, les distributions \(\mathcal{D}^{all}(\theta)\) et \(\mathcal{D}^b(\theta)\) sont égales \cite{Efron}.
La largeur de la distribution \(\mathcal{D}^{all}(\theta)\) donne une estimation des fluctuations de l’estimateur \(\theta\) auxquelles on peut s’attendre compte tenu du fait qu’on utilise un échantillon ne contenant que \(N\) éléments. Ces fluctuations sont alors interprétées comme l’incertitude statistique sur l’estimateur \(\theta\). Le bootstrap permet de construire la distribution \(\mathcal{D}^b(\theta)\) et d’obtenir l’incertitude sur l’estimateur \(\theta\) en supposant qu’elle est similaire à la distribution \(\mathcal{D}^{all}(\theta)\), qui n’est pas calculable.
L’incertitude \(u(\theta)\) sur l’estimateur \(\theta\) est obtenue directement à partir de l’écart entre \(\theta_i\) et la moyenne de \(\theta_b\) ainsi que des de l’écart type de \(\theta_b\). Les échantillons \(E_b\) de bootstrap étant obtenus directement à partir de l’échantillon initial, l’incertitude sur l’estimateur \(\theta\) est obtenue sans ajouter d’information supplémentaire à l’échantillon initial. Elle est donnée par :
$$ u(\theta) = \sqrt{(\theta_s - <\theta_b>_{N_b})^2 + \sigma_{N_b}^2} $$
La valeur de l’écart entre \(\theta_i\) et la moyenne de \(\theta_b\) est généralement très faible et l’incertitude sur \(\theta\) est alors directement reliée à l’écart type \(\sigma_{N_b}\) qui quantifie les fluctuations de \(\theta_b\) autour de \(\theta_i\).
Références
- B. Efron, Bootstrap Methods: Another Look at the Jackknife, Ann. Statist., 7 (1), 1 - 26, 1979
- A.R. Henderson, The bootstrap: A technique for data-driven statistics. Using computer-intensive analyses to explore experimental data, Clinica Chimica Acta, 359 (1-2), 1-26, 2005