Présentation
Tout le monde connaît le jeu du morpion ou Tic-Tac-Toe dont le but est de créer en premier un alignement de trois symboles identiques (croix ou ronds le plus souvent). Il existe une version originale de ce jeu qui se base sur des principes faisant appel à la mécanique quantique. Dans cette version quantique, les coups des joueurs sont des superpositions des coups du jeu classique. Le jeu a été inventé par Allan Goff et Novatia Labs. Il existe une page wikipedia en français sur laquelle vous trouverez les articles originaux (en anglais) concernant le jeu et qui explique les règles.
Cette notion de superposition est illustrée par l’histoire du chat de Schrödinger. Lorsque le chat de Schrödinger est enfermé dans une boîte, il peut se trouver dans deux états : il est éveillé ou endormi (mort ou vivant pour les versions plus morbides). Dans notre vision classique du monde, le chat est soit éveillé, soit endormi. En mécanique quantique, le chat est décrit par les deux états à la fois, il est éveillé et endormi en même temps ! Il existe alors une probabilité qu’il soit éveillé ou qu’il soit endormi. C’est le premier principe utilisé dans le jeu, à savoir que chaque joueur va jouer dans deux cases (deux états). Chaque coup est donc une superposition de plusieurs (deux) coups.
Pour savoir si le chat est éveillé ou endormi il faut ouvrir la boîte. Là encore un phénomène quantique se manifeste. En ouvrant la boîte on observe dans quel état est le chat, on fait une mesure. Le chat n’est donc plus décrit que par un seul état, il est soit endormi soit réveillé. On appelle ce phénomène une réduction, car le chat, initialement décrit par plusieurs états, est maintenant dans un seul état bien déterminé. Ce second principe est également utilisé dans le jeu pour déterminer dans quelles cases les coups ont été joués.
Le dernier principe utilisé dans le jeu, également le plus complexe, est celui de l’intrication qui provoque la mesure dont on vient de parler et donc une réduction. En mécanique quantique, deux particules sont dites intriquées lorsque leurs états dépendent l’un de l’autre. Reprenons l’exemple du chat de Schrödinger et supposons qu’il y a maintenant deux chats qui peuvent tous les deux être soit éveillés, soit endormis. Si les états de ces deux chats sont intriqués lorsqu’on mesure l’état de l’un, cela va imposer l’état de l’autre. Par exemple, si le premier chat est éveillé, le second le sera aussi (en supposant que les deux chats sont nécessairement dans le même état car l’un réveille l’autre). Ce qui est remarquable, c’est que ce principe s’applique même si on sépare les chats suffisamment pour qu’ils ne se voit plus ! Dans le jeu, lorsque plusieurs cases sont reliées, intriquées, cela provoquera une mesure. Pour rappel, chaque joueur a joué dans deux cases. Les cases sont intriquées lorsqu’il est possible de faire une boucle en suivant les paires de cases qui ont été jouées. Un joueur doit alors décider dans quelle case le dernier coup a effectivement été joué, c’est la réduction. Cela va induire des réductions en cascade déterminant les différents coups.
Un exemple
Essayons de comprendre sur l’exemple ci-dessous. Au coup numéro 8, le joueur bleu (ronds) forme une boucle de cases intriquées. Cette boucle est matérialisée par les pointillés rouges. Cette boucle, provoque une mesure et donc une réduction.
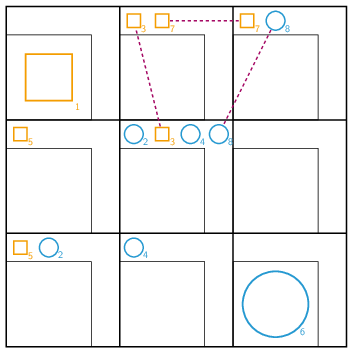
Le joueur orange (carrés), choisit alors de localiser le coup numéro 8 du joueur bleu dans la case de droite de la première ligne. Le coup numéro 8 qui était une superposition de deux cases est donc réduit à une seule case. Cette réduction a des conséquences sur les autres coups. Le coup numéro 7 (carrés orange) ne pourra pas se localiser sur la case de droite de la première ligne. Il se localise donc sur la case centrale de la première ligne. Cela conduit le coup numéro 3 (carrés orange) à se localiser sur la case centrale de la deuxième ligne et les coups 2 et 4 (ronds bleus) à se localiser respectivement sur la première et deuxième cases de la troisième ligne. De même le coup numéro 5 (carrés orange) se localise sur la première case de la deuxième ligne. On obtient donc la situation suivante :
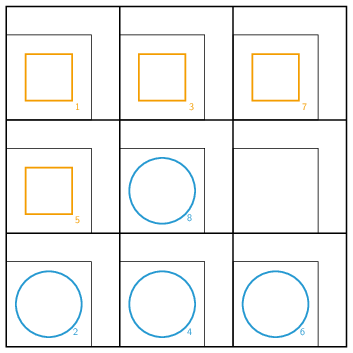
Conclusion : La partie se termine sur un match nul, un partout ! En effet, c’est au joueur bleu de jouer mais il ne peut jouer que dans la troisième case de la deuxième ligne ce qui ne changera pas le score.
Matériel pour jouer
Voici deux documents qui peuvent vous aider pour jouer :
Vous pouvez plastifier le plateau à imprimer en A3 et ensuite jouer avec des feutres effaçables.
Voir la quantique ?
Voir la quantique ? est une conférence de Julien Bordroff du Laboratoire de Physique des Solides de l’Université Paris sud 11. Dans cette conférence, il présente la mécanique quantique et plusieurs expériences permettant de mettre en évidence des phénomènes quantiques.
Je vous recommande également les vidéos disponibles sur le site tout est quantique qui expliquent de façon simple les phénomènes quantiques présentés sur cette page.